此文发表于2018年6月《教育研究与评论》（小学教育学）

 

在 “拐弯”处缓行

                ——关于低年级数数和背乘法口诀的思考

戴磊

（苏州市新庄小学校  江苏  苏州  215000）

【摘要】 数数和背乘法口诀是低年级数学教学必做的两件事。数数是数列的、加减法的启蒙，背乘法口诀是熟练计算表内乘除法的前提，两者都是以后运算教学的基础。教师应有效利用学具，让学生理解、掌握“拐弯数”和“拐弯背”。不用记忆代替思考，不让背诵掩盖本质，让学生且记且思索，为运算能力的发展打下坚实的基础。

【关键词】数数  乘法口诀 拐弯数  拐弯背

数数和背乘法口诀是低年级数学教学必做的两件事。数数是数列的、加减法的启蒙，背乘法口诀是熟练计算表内乘除法的前提，两者都是以后运算学习的基础，其重要性不言而喻。对于数数和背乘法口诀，死记硬背并不能完全奏效，而“拐弯”，不失为一种好方法。

一、“拐弯数”：以直观表象辅助数数的理解

刚入学的学生在学前基本都有数数的经验，数数对他们来说似乎很简单。因此，很多教师在低年级教学中常常忽视数数的教学，或者即使有数数的教学，也停留在学前类似于念童谣的阶段，对数数缺乏深刻的认识。对于低年级学生来说，数数是认识数的抽象过程。教师应充分利用学生的已有经验，让学生在数数的过程中有思维的投入，而非 “念童谣”，即引导学生知道在数什么，知道数的结果，通过反复抽象来体验数是数出来的。

所谓“拐弯数”，是指在数数过程中，从接近整十整百的数数到整十整百的数（如图1所示）。

图1

在实际教学中，“拐弯数”无疑又是数数中的难点。因此，在“拐弯数”时，教师需要放慢速度，不断加强操作和演示。例如，从279到280，要通过将小棒满10根捆成一捆的动作演示，使学生直观感受 “满十进一”；从699到700，更要放慢速度，通过两次“打捆”（10个一变为1个十，10个十变为一个百），让学生直观感受计数单位之间的十进制关系。通过形象的打捆等直观表象，加深学生对十进制的理解，为学生掌握“拐弯数”的方法提供形象支撑。在这个过程中，操作和理解成为一个相互交替、相互交融的认知活动。

可以用来辅助理解“拐弯数”的直观表象有很多，如有结构的实物、计数器、数位表、数轴等，这些都可以作为视觉形象支撑。其中，有结构的实物最为直观形象，如图2中的小棒。计数器的运用已经有了对于数位的抽象理解，并含有的一定的位值制思想，如图3。数位表是比计数器更进一步的抽象，如图4。半形象、半抽象的数轴距离数的抽象越来越近，如图5。连续数数可以为学生理解加减运算打下基础，往前继续数就是加，“拐弯数”相当于进位加法；往后倒着数就是减，“拐弯数”相当于退位减法。这些直观表象逐步抽象，有助于学生循序渐进地认识数数是怎么回事，进而深刻理解十进制和位值制。再进一步抽象，将数轴隐去，便形成了数列，如图6。仔细观察，这类包含“拐弯数”的按规律填数正是学生按顺序数数练习的“触礁区”。显然，“念童谣”式的数数是有口无心的，一旦脱离情境，对类似的填数练习帮助不大。

 

 

 

 

 

图2                            图3

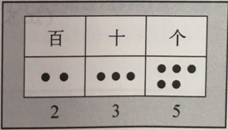
图4

      10（ ）（ ） 13  14 （ ）（ ）（ ）18  19 （ ）

图5

 

	（1）707，708，709，（     ），（         ）。 （2）270，280，290，（     ），（          ）。 （3）980，985，990，（     ），（          ）。 （4）503，502，501，（     ），（          ）。

 

 

 

 

 

 

图6

直观表象不管它有多么鲜明，都不是教学目标，而仅仅是手段。教师需要通过这些表象的操作和演示，在“拐弯数”时放慢速度，由浅入深，帮助学生循序渐进地抽象，促进学生深刻思考。例如图6的（1）和（2）中，从709到710，从290到300，要经过一次打捆；（3）中，从995到1000，要经过两次打捆；（4）中，从500到499，要经过一次拆捆。

由此可见，即使简单如数数，在教学中也要有庖丁解牛的眼光。之后的加减法，特别是进位加法和退位减法，显而易见可上溯至“拐弯数”的打捆和拆捆。“拐弯数”的价值不容小觑。

二、 “拐弯背”：沟通乘法口诀与乘法意义

苏教版小学数学二年级上册中，乘法口诀表一共有45句（如图7）。乘法口诀的背法主要有三种顺序：横着背，竖着背，“拐弯背”。在教学中，教师大多会要求学生横着背和竖着背，却容易忽视“拐弯背”的价值，认为“拐弯背”只是横着背和竖着背的简答组合。

 

 

 

 

 

 

                         

图7

所谓“拐弯背”，是指在乘法口诀表中按照横行背某个数的乘法口诀，背到最后一句时，拐一个直角弯，继续背，背到该数与九相乘的口诀为止。

例如，“拐弯背”六的乘法口诀， 从“一六得六”背到“六六三十六”，再拐个弯背“六七四十二”“六八四十八”“六九五十四”。

横着背，与授课顺序一致，第几行就是几的乘法口诀，后一句总比前一句增加几。竖着背，是几的竖列，下一句就比上一句多几。“拐弯背”，从1到9的口诀都有九句，关于几的口诀就逐渐增加几。“拐弯背”在形式上可以看作横着背与竖着背的结合，但这种结合并不是两种背诵方式的简单叠加，而是乘法意义的融会贯通。

以“二三得六”为例，既可以理解为2个3相加得6，也可以理解为3个2相加得6。同一句乘法口诀，虽然结果相同，但其表示的乘法意义不同。经验表明，只会横着背口诀（如图8），学生通常偏向于几个3相加得几的思考；只会竖着背口诀（如图9），学生则倾向于思考3个几相加得几。受到小数在前、大数在后的顺向思维影响，学生习惯于把乘法口诀理解为“小数”个“大数”相加得到结果。再加上授课顺序的负迁移，学生对横着背最为熟悉，常把竖着背看作横着背的二次记忆。

 

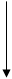
图8

 

图9                  图10

而“拐弯背”（如图10）则强化了乘法口诀与乘法意义之间的联系，把横着的想几个3相加得几延续下去，把竖着想3个几相加得几转化为想4个3相加得几、5个3相加得几……9个3相加得几。因此，教师应在此处放慢速度，借助直观的数线模型（这类模型可以有很多形式，图11仅为一例），引导学生理解几个几个地往前数就是乘。

 

 

 

                                             

图11

由此可见，“拐弯背”是基于横着背和竖着背的更高要求的背乘法口诀方式，它要求背得更熟练、更透彻、更灵活。 “拐弯背”的价值不容小觑，它既能解决表内乘法的基础运算及变式运算，又能对学习除法试商（尤其是有余数的除法）做铺垫。

在教学中经常会遇到一些不等式的括号中最大能填几的练习，如在不等式（）×6＜45的括号里最大能填几，使不等式成立。学生一般会在头脑中搜索与6有关的乘法口诀，再考虑其得数小于45且最接近45。常填错的学生，排除乘法口诀不熟练的，往往是受了横着背的影响，局限于6的六句乘法口诀，即从“一六得六”到“六六三十六”。而熟练掌握“拐弯背”的学生，通常很快能从“六六三十六”拐到“六七四十二”上，从而填出正确答案7。

又如，对于40÷5，有的学生一看到除数是5，就很自然地去背5的乘法口诀，从“一五得五”背到“五五二十五”，只有5句。而且在教材中，5的乘法口诀也就只有这5句，只有在8的乘法口诀里，才有“五八四十”。如果学生经常练习“拐弯背”，就能够顺利地将5的乘法口诀拓展到与5有关的乘法口诀，通过除数5快速地从8的乘法口诀中找到答案。实践证明，“拐弯背”在除法试商时发挥着重要的作用，尤其是所试商大于除数的除法以及有余数的除法。如前所述的“在不等式（）×6＜45的括号里最大能填几”，其实就是45÷6试商的一种变形。给学生补上“拐弯背”一课，对于提高除法试商的正确率和速度都有很好的作用。

因此，“拐弯背”作为一种背诵乘法口诀的补充方式，是沟通横着背和竖着背的桥梁，能更有效地整合学生记忆中的乘法口诀，进而帮助学生深刻理解乘法口诀和乘法意义及二者之间的联系，在以后运算乘除法时能够更准确、更快速、更灵活。我们在教学时不应忽视“拐弯背”。

综上所述，低年级数数和背乘法口诀时，不用记忆代替思考，不让背诵掩盖本质，而要引导让生且记且思索，为运算能力的发展打下坚实的基础。

 

参考文献:

1. 魏智渊.苏霍姆林斯基教育学[M]. 北京：文化艺术出版社，2013.

2. 李星云.小学数学专题研究[M]. 苏州：苏州大学出版社，2001.

3. 王光明 范文贵.新课程标准解析与教学指导(小学数学)[M]. 北京：北京师范大学出版社，2012.

4. 张大均.教育心理学（第二版）[M]. 北京：人民教育出版社，2004.

 

作者简介：戴磊，女，汉族，1982年生，江苏省苏州市人   大学本科   中小学一级教师

通讯地址：江苏省苏州市新庄小学本部   邮编：215008   电话：13776019878