此文于2018年7月获市教科院论文一等奖

 

例谈数学思想在课堂中的落实

                  ——基于庖丁解牛的艺术视角

戴磊

（苏州市新庄小学校 江苏 苏州 215008）

【摘要】数学思想蕴涵在数学知识形成、发展和应用的过程中。因此，数学思想的教学需要在进行知识教学的同时将思想方法渗透其中。如果把数学思想的教学看作解牛之道，那么就要找到学生学习的“骨节”处，如在建构数学概念、发现与证明数学结论、寻找数学解题思路中，融入数学思想这把“无厚之刃”，在不知不觉中分析和解决问题。

【关键词】数学思想  庖丁解牛  渗透教学

《义务教育数学课程标准(2011年版)》关于课程的总目标中指出，“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必须的数学的基础知识、基本技能、基本思想、基本活动经验。”而“数学思想蕴涵在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括。”[[1]]从何处入手呢？如果把数学思想的教学看作庖丁解牛[[2]]之道，那么就要找到学生学习的“骨节”处，融入数学思想这把“无厚之刃”，于不知不觉中分析和解决问题。

一、在建构数学概念中渗透数学思想

影响小学数学概念学习的主客观因素很多。学生已有的知识经验、学生的抽象概括能力和感性材料或感性经验是其中的三种主要因素，也是渗透数学思想需要考虑的方面。下面是一位老师教学“减法”的片段，从中我们可以对抽象思想、建模思想有更明了的把握。

【案例1：减法】[[3]] 

出示情境图（如图1）

师：谁来说一说第一幅图，你看到了什么？

生：从图中我看到了有5个小朋友在浇花。

师：第二幅图呢？ 

生：有2个小朋友去取水了，剩下3个小朋友。

图1

师：谁能把两幅图的意思连起来说一下？ 

 

生：有5个小朋友在浇花，走了2个，还剩下3个。 

师：同学们观察得很仔细，也说得很好。根据这两幅图的意思你能提一个数学问题吗？

 生：有5个小朋友在浇花，走了2个，还剩几个？

生（齐）：3个。 

师：对的，下面请大家用圆片代替小朋友将这一过程摆一摆。（教师一边巡视一边指导学生摆圆片，并指名一生上台演示。）

师：（指着情境图和所摆圆片强调）5个小朋友在浇花，走了2个，还剩3个；从5个圆片中拿走2个，还剩3个，都可以用同一个算式——（学生齐接话：5-2=3）来表示。（在圆片下板书：5-2=3）

生齐读：5减2等于3。 

师：谁来说一说这里的5表示什么？2、3又表示什么呢？

……

师：同学们说得真好！其实在我们的生活中有许多这样的数学问题，5-2=3还可以表示什么呢？请同桌互相说一说。

生1：桌上有5瓶牛奶，喝掉2瓶，还剩3瓶。

生2：树上有5只小鸟，飞走2只，还剩3只。

……

      这是苏教版一年上册的教学内容，此时学生正属于前运算阶段（表象或形象思维期（2～7岁））和具体运算阶段（初步逻辑思维期（7～12岁））[[4]]的转折点，这一时期的儿童一般还只能依赖具体的事物或形象进行运算。

一般的教学是: 教师出示情境图后先让学生认真观察两幅图，说一说从图上看到了什么；再指名学生说说图意“有5个小朋友在浇花，走了2个，剩下3个”；然后提问“你知道怎样列式吗”，学生回答“5-2=3”后教师板书“5-2=3”。接着就教学减号及其读法。

这样的教学，对“5-2=3”而言，它的作用就是一道具体的减法式题，对教师而言，其目光就局限于知识传授，学生学习减法的目的，只要会算一道道减法题就可以了，没有真正获得减法意义的精髓，这是教师在“砍骨”也。但案例中的教学，教师在此基础上又给予了合理充分的展开，既有着眼于学生抽象概括以及举一反三的学习能力的培养，又有同步的数学建模思想的渗透，更加重视学生数学学习的本质，视野开阔。而且这个过程适切低年级儿童数学学习的特点逐渐铺展，以自然、生动而非简单、生硬的方式进行。从具体形象的生活情境出发，先形成初步的外在认知，再通过操作加以内化感知，然后借助已有的知识经验予以强化拓展，进一步提升思维品质的广度和深度，赋予 “5-2=3”更多的儿童化的模型意义。学生这样学习减法，侧重于理解减法是怎么回事，对减法的数学结构“□-□=□”有了丰富的认识。这是教师“游刃于骨间”也。

 二、在发现与证明数学结论中浸润数学思想

美国心理学家、教育学家布鲁纳认为：学习者在一定的情境中，对学习材料的亲身经验和发现的过程，才是学习者最有价值的东西。[[5]]这个最有价值的东西应该也包含着数学思想。下面，我们以乘法分配律的教学为例，来看一看这条重要的运算律是怎么被学生富有创造性地发现与证明的。

【案例2：乘法分配律】[[6]]

（一） 发现

　　提问：校服每件上衣62元，每条裤子37元，全班35个人，每人一套校服，需要花多少钱？先不计算，说一说你是怎么列算式的。

　　交流：每一套校服的钱乘总的套数：（62＋37）×35；或者所有上衣的钱加上所有裤子的钱：62×35＋37×35。

　　猜想：这两个算式的结果会怎样？动手算一算，是否真的相等？  

　  学生计算后，教师在黑板上板书：（62＋37）×35＝62×35＋37×35。然后出示两个类似的问题，用类似的方法再得到两个等式：（4＋2）×25＝4×25＋2×25，（10＋8）×50＝10×50＋8×50。

观察这三个等式，你有什么发现？请用自己的话说一说。

　　（二） 表述

　　学生用自己喜欢的方法，尝试用文字、符号等不同表达式表述乘法分配律。

　　（三） 证明

　　师：大家的发现正确吗？

　　生：正确。我举了几个例子，都验证了它。

　　生：不一定。找不到反例，只能说明它正确的可能性很大，但不能说明一定正确。

　　师：怎么才能说明这个结论一定正确呢？

　　生：除非我们能用学过的数学知识来证明它正确。

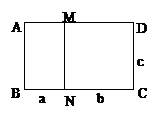　　师：对！在数学上肯定一条结论，需要凭借证明。以（a+b）×c=a×c+b×c（a、b、c都是大于0的自然数）为例，你能证明它吗？

图2

　　生：可以用乘法的含义来证明。根据乘法的意义，（a+b）×c表示c个（a+b）的连加，去掉括号，就是c个a的连加，再加上c个b的连加，根据乘法的含义，就是a×c+b×c。（师根据学生的叙述板书）

 

　 生：可以用长方形的面积来证明。如图2所示，长为a+b、宽为c的长方形ABCD的面积为（a+b）×c，也可以是两个长方形ABNM与MNCD的面积和，即a×c+b×c，从而（a+b）×c=a×c+b×c。

　　师：这样，我们就可以确定（a+b）×c=a×c+b×c是正确的。我把这个等式变成c×（a+b）=c×a+c×b，你说它正确吗？

　　生（众）：正确。

师：我们把这个规律叫做乘法分配律。现在，同学们用自己的话再说一说什么是乘法分配律。

教学片段中，虽然两次让学生表述乘法分配律，但是两次的着力点不同。第一次，教师经由数学问题的解决，让学生观察得到的多个数学事实，启发学生提出猜想，顺势形成对猜想的初步表述。第二次，教师着重引导学生对猜想进行验证。学生很自然地举出很多正例，以此使原来的猜想变得更为可靠，学生合情推理的能力获得发展。后刀锋一转，让学生思考是否可举出反例推翻原来的猜想，相机补充演绎论证，二次表述更融入了学生对乘法分配律意义的肯定和理解。

深观上述教学，数学推理思想、符号思想、数形结合思想在其中穿插运用，交织体现，显然推理思想是最主要的。数学学习中的猜想—验证、肯定一个结论需要给出证明，否定一个结论可以举出反例……这些正是数学思想在告诉学生进行数学小研究时怎样思考、从什么角度思考，也从一个侧面看出教师在发挥主导作用渗透多种数学思想时，要合理把握关系，注意“游刃在筋肉、骨骼”等不同学习阶段间的轻重、快慢、进退……

　　三、在寻找数学解题思路中涵养数学思想

在数学解题研究领域，美国数学家和数学教育家G·波利亚无疑有着十分重要的贡献。他有感于学生解数学题时常常困惑怎么才能想出一个好的解法，于是亲自实践研究，寻找答案，专门写了《怎样解题》一书。其中的“怎样解题”表详细分析了求解各种数学问题时的思维过程，清楚列出了包括 “弄清问题”、“拟定计划”、“实现计划”和“回顾”四大步骤的解题全过程。对“拟定计划”的分析是最为引人入胜的。细细体会，解题表不仅折射出重要的数学思想——化归、变换思想，而且蕴涵着各种数学思想的源泉。仔细研究它对于教师帮助学生学会数学地思维，启发学生去联想，同时涵养数学思想有着很好的启示作用。

例如，下面的一段会话式教学，可以让我们从中一窥用解题表解题的部分范例。

【案例3：一个作图题】在给定的三角形中作一个正方形，使正方形的两个顶点在三角形的底边上，另两个顶点分别在三角形的另外两条边上。[[7]]

“未知的是什么?” “一个正方形”

“已知数据是什么?” “一个给定的三角形，其它没有。”

“条件是什么?” “正方形的四个角在三角形的边上，两个在底边上，其余两边各有一个。” 

“是否可能满足条件?” “我想如此，但不太有把握。” 

“看起来，你解此题并不太容易。如果你不能解决所提问题，首先尝试去解决某个与此有关的问题。你能满足部分条件吗?” “你说部分条件是什么意思?” 

 “你看，条件与正方形的所有顶点有关，这里有几个顶点?” “四个。” 

“所谓部分条件涉及的顶点数应当少于四个。什么样的部分条件容易满足?” “两个顶点在三角形边上，甚至三个顶点都在三角形边上的正方形，是容易画出来的!”   

图3

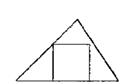
“画张图!” 学生画出图3。

 

“你仅仅保留了部分条件，同时你舍去了其余条件。现在未知的确定到了什么程度?” “如果正方形只有三个顶点在三角形的边上，那么它是不确定的。”

图4

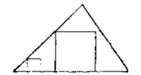
“好!画张图。学生画出图4。

 

“你的正方形的三个角在三角形的边上，但第四个角还不在它应该在的地方。正像你说的，你的正方形是不确定的，它能变化；第四个角也是这样，它怎样变化?”

……

“你可以用实验的办法试试看。按照图中已有的两个正方形的画法，去画出更多的三个角在边上的正方形，画出小的正方形与大的正方形。第四角的轨迹看起来像是什么?它将怎样变化？

教师已把学生带到非常接近于答案的地方。如果学生能猜到第四个角的轨迹是一条直线，他就解出来了。

这个案例通过一连串建议性或启发性问题，适时地化归或变换学生的思维，让学生逐层提升，拾级而上，一步一步地向答案的内核逼近。学生在教师搭建的阶梯下，逐步受归纳推理、极限思想等的洗礼，形成数学经验的积累，由此可见，数学思维方式的养成，数学思想的建立，需要经历一个比较复杂的过程，需要教师长时间的不懈努力和持续渗透，学生才能经历一个从朦胧到清晰的体悟过程，继而使用默会的数学思想。这一点正像庖丁的反复“解牛”，不断悟“道”一样，教学相长而厚积薄发，互臻于得心应手的境界。

衡量一个学生的数学素养，不仅要关注他所知道的数学知识有多少以及他能解多少题，更要关注他对数学精神思想的领会和潜意识的使用。而掌握数学思想方法，也是作为一个数学教师的重要修养，需如庖丁心有“全牛”一般来传道授业解惑。我们需要站在高观点，用自己的深入理解，渗透在课堂教学之中，学生才能受到数学思想的熏染，方能到达数学的灵魂深处。

 

【参考文献】